Back to the Main Entrance
Eratosthenes Got the Circumference of the Earth
by Klaus Kohl
- One historic source-
- rolled by the mill of instruction-
- again and again-
- this remained...
"Eratosthenes by noon of June 21, measured the shadows of the obeliscs in Syene (Assuan nowadays) and Alexandria. In Syene the obelisc had no shadow, in Alexandria the angle of the shadow was 7° 12'. As Eratosthenes assumed the earth as a sphere and (by mistake) Syene being 5000 stadia south of Alexandria he calculated from that a circumference of the earth of 250000 stadia..."
When I called into internet: "Yahoo! Eratosthenes!" it shouted back by umpteenthousand: "Here I am!!".
Even after I had reduced the search in German to "Eratosthenes" and "Erdumfang" (Circumference of Earth) more than 500 answers were reflected.
And there I should contribute new facts? A hobbyist without any humanistic education? - Let us see.
But what at all have I to deal with Eratosthenes?
Physics lessons - metric system - the meter just 200 years old, and what they have to learn: the meter should be the ten millionth part of the earth quadrant.
I don't mind - better understandable (but less precise): The 40 millionth part of the circumference of the earth, measured over the poles and passing Paris.
Such facts are not preached by me as adorable truth - but I ask:
- Why did they want to measure it?
- How did they do it?
Well, I obviously show the fact, that a measurement of that kind - not by Paris - had been executed 2000 years before. Complete surprise! Thus I feel allowed to leave the curriculum and do instead of this some sky investigation - antique, without telescopes, satellites and so on, merely what they can see by themselves.
Ancient astronomy - the very young, sensational astronomy indeed! There was a lot to discover and they discovered a lot!...
It is known the sources about Eratosthenes' measuring of the earth are scanty.
The most detailed description we have has been made by Kleomedes.
But about Kleomedes we know much less than about Eratosthenes.
According to these difficulties the opinions of Eratosthenes' occupation on June 21, "anno dunno" (about 220 a.C.?) are very different.
Many speculations crept into school books, often frankly marked as speculations.
Speculating is allowed, but the result should withstand a critical examination.
Sometimes is claimed Eratosthenes made his observation as a proof -eventually as first- that the earth is a sphere. That's junk, obviously.
When I speculate too, then not only trying to get closer to historic facts but also I want to show how ingenious this idea might have been.
By its brilliancy it has still today a pedagogical value and - if my speculation is not queer at all - it may show the original idea of the scientist.
The Kleomedes report (sorry, still in German) shows a soft aftersound.
How -according to schoolbooks- could Eratosthenes have proceeded?
- Was Eratosthenes in Syene to get the idea there -
- or has he collected all by brooding at his writing desk in the Alexandria library? -
- And how did he get the distance from Alexandria to Syene?
Which descriptions of the experiment can you read mostly today?
- Two obeliscs, one in Syene, the other in Alexandria, possibly used there as sun dials. -
- No obeliscs, but rods (gnomoi) on a horizontal support (distinct sun dials) -
- water pit (dried out?) in Syene, obelisc or gnomon in Alexandria -
- water pit or gnomon in Syene, scaphe in Alexandria.
What is speaking in favor to the obelisc(s)?
They stood around everywhere - perhaps at least besides they were used as sun dials.
"Each village had at least one, like nowadays a war memorial and a traffic circle".
But are we not reducing our imagination of ancient Egypt to obeliscs, pyramids and mummies?
What is speaking against?
In Syene: Who will at highest hottest noon look at an obelisc to see that it has -for some minutes- no shadow?
At all: If we consider the shape of an obelisc we will agree that it is difficult up to impossibility to see a shadow of the peak at a sun azimute of more than 85°.
What I know of Egyptian obeliscs: They normally have the shape of a -however very steep- pyramid socket with a flatter pyramid on it.
An obelisc thus will have a shadow when the sun is distinctly out of zenith and a shadow of the peak can be not earlier detected before the height of the sun is distinctly less then 60°.
At the end - and this is settling it - to evaluate the length of the shadow you have to know exactly the height of the obelisc's peak.
Thus the shadow of an obelisc for the execution of Eratosthenes' measurement is completely useless but you can't thrash it out of the literature.
Many publication are aware of these arguments and instead of an obelisc there is a vertical rod, a "gnomon" witch shows at noon in Syene no shadow at all but in Alexandria a small one what can be measured.
This is the way Kleomedes mentions.
But... with a stick that has no shadow - in winter you won't lure your dog from behind the oven and in summer no Egyptian from his shady shelter.
"Oh, Achmed! Wake up, look! That stick has no shadow! We have to communicate it to the mayor, the sheriff!"
It is really a pity not to know anything of Achmed's answer... we could be familiar with some suitable expressions from Ptolemaen Egypt...
But indeed many citations mention that vertical stick, at least in Alexandria.
And in all by now rather common school experiments to this theme on June 21, at noon (I hope they take local time!) a meter stick is put to the ground vertically and the length of its shadow is noted.
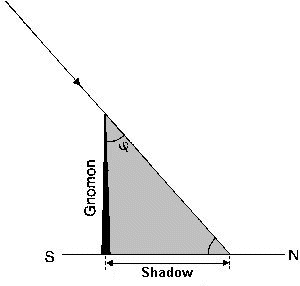
Gnomon
By Internet a school south or north of this location is contacted: "We have this, what did you get?
The distance is taken from the atlas
The remainder is home work: "Radius of the earth until tomorrow!"
That`s it - Internet makes it possible - an important reason for "Schools to the Net!" (at the Wagenschein era still letters had to be used.)
It's simple, or?
A meter stick? Comfortable, but not necessary - only the proportion shadow/height is important:
tangent alpha, here it comes! - Get your calculators!
STOP!
Of course Eratosthenes had no calculator, but goniometric functions too were a later invention.
Thus the students should guess another solution...
To draw it by scale and take the angle from there might be the most useful suggestion - let us hope that it had not to come at last by the teacher!
Might Eratosthenes have gone this way?
Owned he already a protractor?
But let us go by mind to the tropic, to Syene.
It lies not exactly on the tropic but sufficient enough to become famous this way and sufficient enough to be dazzled when you (or your wife/daughter will be dazzled) going for water to the pit at noon at June 21 and look after the bucket thrown into the deep -normally dark- hole. That is not only dazzling, that's a sensation!
That is really another thing than a stick or obelisc without shadow... We can be shure that in these times in Syene the water pits had not dried out, at least not all and pits were used to get water as the Nile water at least by the summer flood would be undrinkable.
It was a sensation found by chance, probably long ago and repeating regularly.
This should be commercialized! - And I assume, it was...
Do you remember the last total sun eclipse and the big fuss about it?
I am shure - each June 21 of our calendar in Syene there was the "big water pit festival market". - And by noon: "Come and look! Only a dime! Look into the pit! Come and look!" This worked some days - in these days. Today the scarce water pits in the surroundings are really dried out and the Assuan Water Corporation works a bit more efficiently but without any sensation.
No obelisc, no gnomon is needed, sun by itself shows from down under that it is in the zenith!
I think Kleomedes/Eratosthenes mentions the gnomon in Syene only to explain his following text.
To go there and make the measuring was not necessary at all. Eratosthenes knew it.
(You may think my fantasy was just running away with me... probably the waterholes in Syene at this time were quite normal pits and not deep shafts as we are used to them today, then all the idea of pit market is make believe - but Eratosthenes was geographer enough to know the sun shining at midsummer noon just vertically on the tropic!)
Maybe in earlier times he himself has taken part at this fantastic celebration and if not yet, then he squatted -a bit sour?- in Alexandria where this never can be seen, too wide in the north!
There the shadow thrown by the gnomon is but the shortest posssible but it is thrown - and where?
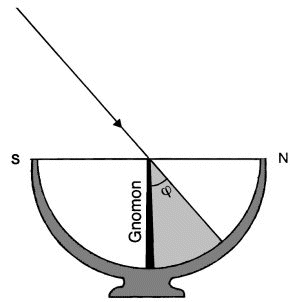
Scaphe (after Dannemann)
Not on the plain surface of a common sun dial but - Eratostehenes could afford or commandeer it - and thus it is expressively described by Kleomedes, a "scaphe", a bowl, a hollow hemisphere, as it was intended to show the vaulted sky over the peak of the gnomon just as middle point of the hemisphere
And this short shadow had the right size to fit fifty times on the rim of that scaphe (probably done by a pair of compasses).
And now the idea!
And this is my speculation in honour to Eratosthenes:
Until now it had been a mere routine work to measure the shadowlength by putting it on the rim of the scaphe. In the moment he got the maximal height of the sun in Alexandria - fifty times did the shadow fit to the rim...
And suddenly the flash: A turn down -worth to M.C.Escher- of the figure:
The hollow scaphe, adapted to consume the hollow-vaulted sky turns to the convex globe!
Both have the same proportions, the same geometrical order!
This new thinking is the sensation:
Heureka!("I got it!" as Archimedes -his contemporary fellow- is said to have shouted running naked by the streets of Syracuse, after he had discovered the laws of buoyancy)
What is valid for that hollow scaphe is equally valid for the earth globe with its curve!
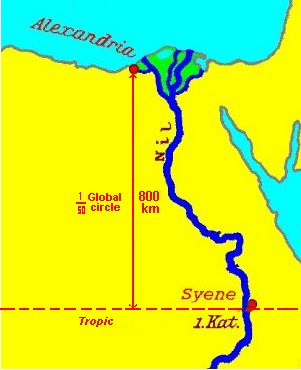
As the shadow in the scaphe fits fifty times to its circumference, the distance between Alexandria and the tropic(!) fits fifty times on the earth circle through Alexandria, the circumference of the globe,
- Knowledge...
- Measuring...
- Combining!
And that is fairly correct.
If we take our atlas and measure the distance between Alexandria and the tropic we get 860 km,
the error is about 8%, 46 or 47 times would have been better.
Or if we look into the encyclopedia, the latitude of Alexandria is 31°13', of the tropic 23°27',
makes a difference of 7¾°, fitting 46½ times into the circle.
Don't care! Do it better!
For my way of instruction now it is essential that by this measuring and its description neither triangle sides nor angles appear, there is nothing but arcs.
Both arcs - in the scaphe as well as on the surface of the earth -
are one fiftieth of the full circle,
This makes the measuring and its evaluation much clearer
.
As Kleomedes gives a detailed description of the laws of angles - I suppose that he did that only to prove the legality of Eratosthenes' deliberation and we may assume that this was done by Eratosthenes in his papyrus, too.
Perhaps Kleomedes had a view of this paper?
The mere measuring had nothing to do with angles in our sense.
The ever and again cited 7.2° or even 7°12' could not have place in the mind of Eratosthenes.
I have got the impression that the long and tiring description of the basics of the measurement had as only goal:
To prove this ingenious idea to a sceptical critical academic public.
According to Euclides: Condition - Assertion - Proof.
At the and of his article Kleomedes resumes:
"The arc in the hemisphere of the scaphe was found as one fiftieth of its circle.
Therefore the distance between Syene and Alexandria must be one fiftieth of the largest earth circle.
The mentioned distance is 5000 stadia, so that largest earth circle is 250 000 stadia."
Stop! - 7.2° never appear in his description!
The result of his measurement should be presented perhaps this way:
"Around the world it is 50 times longer than from here in Alexandria to the tropic, the distance -to make it more visible- to Syene". And not before the second place the statement is put: "And as this distance is 5000 stadia it will be round about the earth 250 000 stadia." And to quarrel on the question how many meters and centimeters the stadium of Eratosthenes really held, has no reason at all as well as the question always combined with it: How exact was the determination of Eratosthenes?
But there is a historic fact: By mistake and/or cleverness during 1½ thousand years the confusion by changing the units and numbers the 250 000 stadia became 180 000 stadia (of what size?) but by this way Columbus could argue the left tour from the Azores to East Asia would be not much longer than from the Lebanon to these Azores...
----------------------------
I had planned to end here, but by the elaboration I began to broode.
I had said:
And that is fairly correct.
and after showing the fault I said - like a bored, exhausted student would say:
Don't care! Do it better!
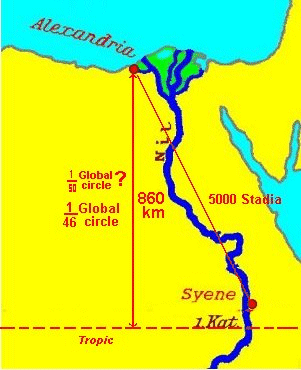
Mistake anyway?
Well, how might that -really remarkable- mistake have happened to Eratosthenes?
His contemporians looked at him as a stickler who would not have been satisfied by making 46 or 47 steps to get around and then round it up to declare: "It's fifty!" (While 48 would have been more practical because its ability to be divided.)
We can be shure: it was exactly 50 and nothing else!
So it has been to short!
We may consider that he got the wrong date or the wrong daytime - but then the shadow should have been even longer, not shorter!
Will the latitudes in the encyclopedia not be valid to the working place of Eratosthenes? No. we can be shure, 60km south of Alexandria, why -even if at this time it was not yet a desert as today- should he have placed his sundial there and give no notice of it and refer to Alexandria?
No, it looks more to be a systematic error which has not been discovred by the writers of today.
Error No. 0: - The banality -
The rod was slanting.
Could Eratostheens adjust it to half a degree, a hundredth of a Radian?
If he could he would have done.
How he could do it we do not know.
And perhaps anything else of the scaphe was no precision work?
Error No. 1 - The stupid one -
Eratosthenes measured off the Gnomon and did not consider its thickness. So half the diameter of the gnomon was missing to the length of the shadow.
Really a stupid error - I think, too stupid for Eratosthenes.
Error No. 2 - The interesting one -
If we put the question: What did the shadow look alike?
we should ask: How was the gnomon's peak formed?
How could it be formed?
How should it be formed as an optimal gnomon for a scaphe?
Did Eratosthenes know that?
We will just see: He knew!
(A gnomon with a diameter of 1% of the radius of the scaphe and a hemispheral peak -middle of the gnomon's hemisphere is the center of the scaphe's hemisphere- gives always a pointing shadow of the sun with a distinctive peak at the right place, as the angular diameter of the sun is a hundredth of a radian.)
Possibility Nr. 3: No error, at least to Eratosthenes:
He was rightly measuring, and we are wrongly thinking!
How now that?
If the sun stood really as high at the sky as Eratosthenes had measured - then Alexandria laid by these times closer to the tropic than today.
No... - inversed it sounds better:
2200 years ago the tropic laid closer to Alexandria than today.
Indeed we know today something more than the ancient astronomers.
Cosmic conditions are not at all as stable as believed then.
Only the slow orbiting of the earth's axis by a "Platonic Year" (about 25 800 years) had been remarked.
(That we can find North by the Pole Star is a nice concession to our age.)
But the earth's axis performing a slight nodding movement to its orbiting plane, that was detected much later. The Period is about 41 000 years and the amplitude is between 21.9° and 24.3°, by now decreasing.
(A third periodic change may be mentioned: By a rhythm of about 100 000 years the orbit of the earth around the sun stretches and rounds. This might contribute to the ice ages, but it does not affect our considerations
.
This nodding of earth's axis makes a periodic movement of the tropics to and from the equator. The position of the eqator itself is not affected.
With today's precision measuring the position of the tropics at the time of Eratosthenes can be recalculated:
They were about half a degree of latitude farther away from the equator than today!
But it does not need such a large-scale calculation as:
Eratosthenes himself is assigned to the assertion:[1]
"The distance of the tropics to each other is 11/83 of the earth's circle."
By our common measures that would be 47 3/4°, today it is 46°54'.
If we divide this specification of Eratosthenes by 2, the northern tropic will be at 23 7/8° (23°53'), That is 7¼° south of Alexandria and 20 km - 12 minutes of an angle - south of Syene (24°05').
That the tropic in an atlas of today is distinctly off Assuan, the sun there unable to reach the zenith and therefore can never look into that deep pit as it was possible 2200 years ago, that is not the fault of Eratosthenes!
How he had measured this?
probably by the same way as his famous one, but in winter and by putting the difference on the rim of the scaphe counting the rounds he had to make with his compasses - without a protractor - tiring but exact!
In the end he was right!
Eratosthenes got the earth's circumference!
That it is around the globe 50 times as far as from Alexandria to the tropic; did fit by a half percent.
And nothing else Eratosthenes had measured and concluded.
All the rest - the 5000 stadia to Syene and the position of Syene south of Alexandria were estimated.
As a geographer Eratosthenes was aware of the difficulties and incertitudes of such statements at his time.
To harp on it by censoring and comparing it with the results of our(?) GPS - we should leave that!
The measuring of Eratosthenes was the first reliable determination of a cosmic standard.
Very important because by now only the proportions had been detected.
So it was an enormous progress and its accuracy stayed unsurpassed until 1671 (Jean Picard).
The ingenious idea makes an evaluation simple - but in all schoolbooks the brilliancy is buried by ignorance of the most authentic source
The cutting remark of a snappish expert of the scene:
"School book producers just copy each other!"
--------------------------------------------------
This text goes along a lecture held at a convention of the section History of Mathematics of the Deutsche Mathematiker-Vereinigung (DMV) in Attendorn/Neu-Listernohl May 28, to June 1, 2003
Der Kleomedes-Text is in Internet accessible by:
www.martin-wagenschein.de/K-Kohl/Eratosth/Balss.htm (German translation)
[1] This assignment is occasionally doubted. The report is done by Ptolemaios, and a common interpretation is that Ptolemaios himself had measured it.
But I suppose that if Ptolemeaios had presented his own measuring he would have done it by the now common way of degrees instead of using that complicated fraction.
If on the other side the exact measuring of the tropics would have been impossible before the era of Ptolemaios, the actual statement of Eratosthenes (1/50 of the earh's circle) would have been even more precise. Because from his time to Ptolemaios the tropic would have wandered a bit more to the north!
On the other hand I may not accept that there was a "kabbalistic" reason to put the tropic at 1/15 of the earth's circle. Even the 5000 Stadia from Alexandra to Syene are sometimes interpreted as such a postulate...
There are a lot more inconsistencies: Strabo writes that Eratosthenes gave a circumference of 252000 stadia to get a degree of latitude of 700 stadia - but the dividing of a circle in degrees was at the time of Eratosthenes really uncommon... Finally the philologues quarrel about differences and their interpretation in the Kleomedes text.
Here I want only to emphasize which interpretation I feel to be adequate for physics lessons and further on. That ist was possible this way (and many other ways described are impossible and useless too, that does not mean that I think it had gone this way and no other. It might have gone a total different way!
[Back to the text]





